Circular Collision Detection
Last Updated 4/09/14
Besides rectangles, the most common shape you'll have to deal with is a circle. In the last tutorial we had to use 11 collision boxes for a circle. This tutorial will teach you a more efficient way to handle circles and collision detection.A Circular Collision Detection tutorial with SDL 2 is now available.
#include "SDL/SDL.h"
#include "SDL/SDL_image.h"
#include <string>
#include <vector>
#include <cmath>
This tutorial is going to require the distance formula so we include a header for math.
//A circle stucture
struct Circle
{
int x, y;
int r;
};
We have to create our own circle structure for this program. "x" and "y" are the offsets of the center of the
circle. "r" is the radius.
//The dot
class Dot
{
private:
//The area of the dot
Circle c;
//The velocity of the dot
int xVel, yVel;
public:
//Initializes the variables
Dot();
//Takes key presses and adjusts the dot's velocity
void handle_input();
//Moves the dot
void move( std::vector<SDL_Rect> &rects, Circle &circle );
//Shows the dot on the screen
void show();
};
Here's yet another revision of the Dot class.
Everything is pretty much the same except for two differences. This time we have a Circle structure instead of a vector of SDL_Rects. Also, in the move() function we check collision with a vector of SDL_Rects and a Circle.
Everything is pretty much the same except for two differences. This time we have a Circle structure instead of a vector of SDL_Rects. Also, in the move() function we check collision with a vector of SDL_Rects and a Circle.
double distance( int x1, int y1, int x2, int y2 )
{
//Return the distance between the two points
return sqrt( pow( x2 - x1, 2 ) + pow( y2 - y1, 2 ) );
}
This function we made gives us the distance between given 2 points. This is pretty much the only real math used in
this program.
For those of you using visual studio you may need to type cast those integers to doubles.
For those of you using visual studio you may need to type cast those integers to doubles.
bool check_collision( Circle &A, Circle &B )
{
//If the distance between the centers of the circles is less than the sum of their radii
if( distance( A.x, A.y, B.x, B.y ) < ( A.r + B.r ) )
{
//The circles have collided
return true;
}
//If not
return false;
}
Checking collision between two circles is pretty easy. All you have to do is check whether or not the distance
between the centers of the circles is less than the sum of their radii.
If it is less, a collision has happened, otherwise there's no collision.
If it is less, a collision has happened, otherwise there's no collision.
bool check_collision( Circle &A, std::vector<SDL_Rect> &B )
{
//Closest point on collision box
int cX, cY;
//Go through the B boxes
for( int Bbox = 0; Bbox < B.size(); Bbox++ )
{
This function checks collision between a circle and a vector of rectangles. Checking for collision between a circle
and a rectangle gets a bit tricky. To check if there's a collision between a circle and a collision box, you must
find the point on the collision box closest to the center of the circle.
//Find closest x offset
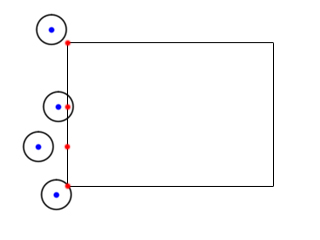
if( A.x < B[ Bbox ].x )
{
cX = B[ Bbox ].x;
}
If the center of the circle is to the left of the box, then the x offset of the closest point is equal to the x
offset of the collision box.

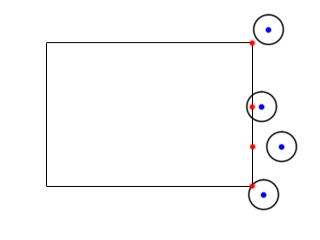
else if( A.x > B[ Bbox ].x + B[ Bbox ].w )
{
cX = B[ Bbox ].x + B[ Bbox ].w;
}
If the center of the circle is to the right of the box, then the x offset of the closest point is equal to the x
offset of the right side of the collision box.

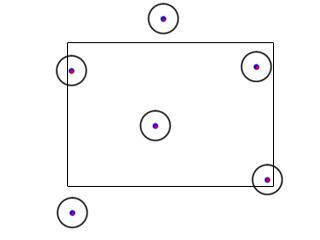
else
{
cX = A.x;
}
If the x offset of the center of the circle is not to the left or the right of the collision box, then the x
offset is inside the collision box.

//Find closest y offset
if( A.y < B[ Bbox ].y )
{
cY = B[ Bbox ].y;
}
else if( A.y > B[ Bbox ].y + B[ Bbox ].h )
{
cY = B[ Bbox ].y + B[ Bbox ].h;
}
else
{
cY = A.y;
}
Then we do the same as above to find the closest y offset.
//If the closest point is inside the circle
if( distance( A.x, A.y, cX, cY ) < A.r )
{
//This box and the circle have collided
return true;
}
}
//If the shapes have not collided
return false;
}
If the point on the collision box closest to the circle is inside the circle, then the circle and the collision
box are overlapped. Here we keep going through all the collision boxes until we find a collision or all of the
boxes have been checked and there is no collision.
//Make the shapes
std::vector<SDL_Rect> box( 1 );
Circle otherDot;
//Set the shapes' attributes
box[ 0 ].x = 60;
box[ 0 ].y = 60;
box[ 0 ].w = 40;
box[ 0 ].h = 40;
otherDot.x = 30;
otherDot.y = 30;
otherDot.r = DOT_WIDTH / 2;
In the main() function we create the 2 shapes the Dot is going to interact with.
//While the user hasn't quit
while( quit == false )
{
//Start the frame timer
fps.start();
//While there's events to handle
while( SDL_PollEvent( &event ) )
{
//Handle events for the dot
myDot.handle_input();
//If the user has Xed out the window
if( event.type == SDL_QUIT )
{
//Quit the program
quit = true;
}
}
//Move the dot
myDot.move( box, otherDot );
//Fill the screen white
SDL_FillRect( screen, &screen->clip_rect, SDL_MapRGB( screen->format, 0xFF, 0xFF, 0xFF ) );
//Show the box
SDL_FillRect( screen, &box[ 0 ], SDL_MapRGB( screen->format, 0x00, 0x00, 0x00 ) );
//Show the other dot
apply_surface( otherDot.x - otherDot.r, otherDot.y - otherDot.r, dot, screen );
//Show our dot
myDot.show();
//Update the screen
if( SDL_Flip( screen ) == -1 )
{
return 1;
}
//Cap the frame rate
if( fps.get_ticks() < 1000 / FRAMES_PER_SECOND )
{
SDL_Delay( ( 1000 / FRAMES_PER_SECOND ) - fps.get_ticks() );
}
}
Here's the main loop, pretty much everything is the same story as before.
I would like to point one thing out.
When we show the other dot, we don't blit the image at its offset. The offset is the center of the circle, so we have to blit the dot image at the upper-left corner. We do this by subtracting the radius from the offset.
When we show the other dot, we don't blit the image at its offset. The offset is the center of the circle, so we have to blit the dot image at the upper-left corner. We do this by subtracting the radius from the offset.